Phân biệt đường phân giác, đường trung tuyến, đường trung trực: cách nhận biết nhanh và dễ nhớ
Việc phân biệt đường phân giác, đường trung tuyến, đường trung trực trong tam giác là kỹ năng cơ bản nhưng rất quan trọng khi học Hình học. Tuy nhiên, nhiều học sinh vẫn dễ bị nhầm lẫn giữa các khái niệm này do chúng có nhiều điểm tương đồng về hình dáng và vị trí. Trong bài viết này, chúng ta sẽ cùng tìm hiểu cách nhận biết từng loại đường thẳng đặc biệt trong tam giác, áp dụng các mẹo ghi nhớ.
Khái niệm cơ bản về ba đường đặc biệt trong tam giác
Định nghĩa đường phân giác
Đường phân giác của một góc trong tam giác là đường thẳng đi qua đỉnh của góc đó và chia góc thành hai phần có số đo bằng nhau. Nói đơn giản, đây là “đường chia góc” – một phần kiến thức quan trọng thuộc chuyên mục kiến thức cơ bản toán học.
- Dấu hiệu nhận biết: luôn đi qua một đỉnh và chia góc tại đỉnh thành hai góc nhỏ bằng nhau.
- Hoàn cảnh sử dụng: Dùng để xác định các tính chất liên quan đến các đoạn thẳng, tỉ số khoảng cách, hoặc tìm tâm đường tròn nội tiếp tam giác.
Định nghĩa đường trung tuyến
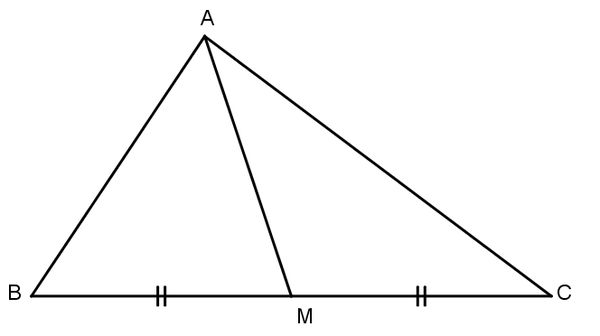
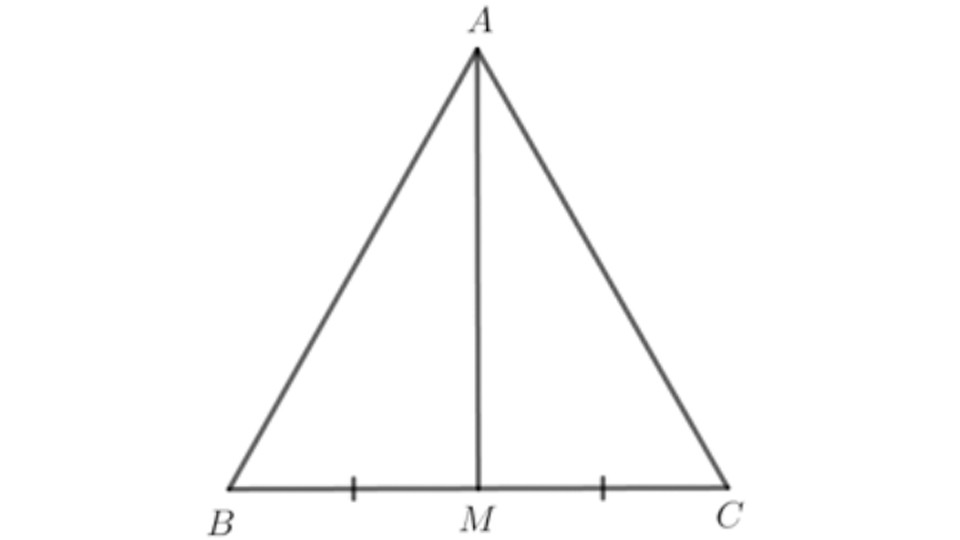
Đường trung tuyến là đường thẳng xuất phát từ một đỉnh của tam giác, đi đến trung điểm cạnh đối diện với đỉnh đó. Đường trung tuyến chia tam giác thành hai phần có diện tích bằng nhau.
- Dấu hiệu nhận biết: Đầu mút là một đỉnh tam giác, đầu kia là trung điểm cạnh đối diện.
- Vai trò thực tiễn: Đường trung tuyến đóng vai trò quan trọng trong các bài toán về trọng tâm tam giác.
Định nghĩa đường trung trực
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc và đi qua trung điểm của đoạn thẳng đó. Trong tam giác, đường trung trực của mỗi cạnh không nhất thiết đi qua đỉnh.
- Dấu hiệu nhận biết: Không dựa vào đỉnh, chỉ xuất phát từ cạnh, vuông góc với cạnh tại trung điểm cạnh.
- Ứng dụng: Giúp xác định tâm của đường tròn ngoại tiếp tam giác như trong các bài học thuộc chuyên đề hình học.
Điểm khác biệt then chốt giữa ba đường thẳng này
Về xuất phát và vị trí
Khi phân biệt đường phân giác, đường trung tuyến, đường trung trực, điều đầu tiên cần để ý là điểm đầu và hướng đi của mỗi đường:
- Phân giác: Xuất phát từ đỉnh, cắt góc tại đỉnh ra hai phần bằng nhau.
- Trung tuyến: Xuất phát từ đỉnh, đi đến trung điểm cạnh đối diện.
- Trung trực: Không đi qua đỉnh, chỉ đi qua trung điểm cạnh và vuông góc với cạnh đó.
Về tính chất hình học
Cả ba đều liên quan đến tính cân bằng (chia đôi, chia đều…), nhưng mục đích khác nhau:
- Phân giác: Chia góc thành hai phần đều.
- Trung tuyến: Chia diện tích tam giác thành hai phần bằng nhau (theo lý thuyết từ chuyên mục dạy con học tốt toán).
- Trung trực: Mỗi điểm trên đường trung trực cách đều hai đầu mút đoạn thẳng.
Mẹo nhận biết nhanh và mẹo ghi nhớ dễ nhớ
Nhận biết qua tên gọi
Đôi khi, tên gọi chính là cách nhận biết hiệu quả nhất:
- Phân giác: “Phân” là chia, “giác” là góc → Chia góc.
- Trung tuyến: “Trung” là ở giữa (trung điểm), “tuyến” là đường thẳng → Nối từ đỉnh đến trung điểm cạnh đối diện.
- Trung trực: “Trực” là thẳng đứng/ vuông góc, “trung” là ở giữa → Đường thẳng vuông góc tại trung điểm cạnh.
Mẹo vẽ và xác định trên hình
Bước 1: Xác định đỉnh và đối diện cạnh.
Bước 2: Xem từ đâu xuất phát, đi về đâu hoặc đi qua đâu.
Bước 3: Dùng thước đo góc, thước kẻ để kiểm tra góc và độ dài phân chia.
Ứng dụng thực tế và ví dụ minh họa
Bài toán trọng tâm tam giác
Trọng tâm là giao điểm của ba đường trung tuyến. Theo nghiên cứu học tập tại Novateen, nếu biết cách xác định trung tuyến, bạn sẽ dễ dàng tìm được trọng tâm, ứng dụng trong tính diện tích hình hoặc các bài toán thực tiễn.
- Ví dụ: Ở tam giác ABC, nối điểm A với trung điểm của BC, đó là đường trung tuyến. Giao điểm các trung tuyến là trọng tâm – điểm cân bằng lý tưởng
Xác định tâm đường tròn nội tiếp và ngoại tiếp
Tâm của đường tròn ngoại tiếp là giao điểm ba đường trung trực, còn tâm đường tròn nội tiếp là giao điểm ba phân giác góc. Nắm chắc cách vẽ, bạn sẽ giải quyết nhanh các bài toán liên quan đến tiếp tuyến, tiếp điểm.
- Ví dụ: Vẽ đường trung trực cho mỗi cạnh một tam giác, giao nhau tại điểm O. O chính là tâm đường tròn ngoại tiếp.
- Ngược lại, vẽ phân giác của từng góc tam giác thì giao điểm sẽ là tâm đường tròn nội tiếp.
Sai lầm phổ biến và cách khắc phục khi học phần này
Nhầm lẫn vị trí, đường thẳng và đặc trưng
Phân biệt đường phân giác, đường trung tuyến, đường trung trực thường nhầm khi:
- Vẽ nhầm đường từ đỉnh xuống cạnh (trộn lẫn trung tuyến với phân giác).
- Quên kiểm tra xem đường đó có vuông góc với cạnh hay không (yếu tố của trung trực).
- Chưa quan sát kỹ các tính chất chia đoạn thẳng hoặc chia góc.
Cách khắc phục: Làm nhiều bài tập, thực hành vẽ hình, tự đặt câu hỏi “đường này chia gì?”, “xuất phát từ đâu?” để rõ đặc trưng mỗi đường.
Áp dụng bài tập thực chiến
Liên tục luyện tập với nhiều dạng đề thuộc các chủ đề kiến thức Toán học, tham khảo các external link như Khan Academy để luyện tập bài tập có đáp án chi tiết, giải thích từng bước.
Lời khuyên để thuộc lòng và không bị nhầm lẫn
Tóm lược các đặc trưng bằng bảng so sánh
| Đường Thẳng | Xuất Phát | Kết Thúc | Chức Năng | Giao điểm là… |
|---|---|---|---|---|
| Phân giác | Đỉnh | Cạnh đối diện | Chia góc thành 2 phần bằng nhau | Tâm đường tròn nội tiếp |
| Trung tuyến | Đỉnh | Trung điểm cạnh đối diện | Chia tam giác thành 2 phần diện tích bằng nhau | Trọng tâm |
| Trung trực | Không qua đỉnh | Vuông góc tại trung điểm cạnh | Các điểm trên đường trung trực cách đều 2 đầu mút cạnh | Tâm đường tròn ngoại tiếp |
Học qua sơ đồ tư duy hoặc hình ảnh trực quan
Vẽ sơ đồ tư duy, ký hiệu rõ màu sắc cho mỗi đường đặc biệt. Màu đỏ cho phân giác, xanh cho trung tuyến, vàng cho trung trực – mỗi lần nhìn hình lập tức liên tưởng tới tính chất của đường.
Giải đáp thắc mắc thường gặp
Đường trung tuyến có bao giờ trùng với đường phân giác không?
Có, nhưng chỉ khi tam giác có hai cạnh liền kề tại đỉnh bằng nhau (tam giác cân) thì trung tuyến vẽ từ đỉnh góc cân sẽ đồng thời là phân giác và trung trực.
Làm thế nào để kiểm tra đường vẽ đã đúng là trung trực?
Hãy dùng thước hoặc êke kiểm tra: điểm vẽ trên cạnh phải là trung điểm, và đường vẽ phải vuông góc với cạnh đó. Vẽ lên từng vị trí, so lại với lý thuyết để tránh sai sót.
Trong một tam giác đều, số lượng giao điểm giữa ba đường này là bao nhiêu?
Trong tam giác đều, ba đường phân giác, trung tuyến và trung trực đồng quy tại cùng một điểm – tính chất đặc trưng của tam giác đều.
Đường trung trực và đường cao có gì giống và khác nhau?
Cả hai đều vuông góc với một cạnh, nhưng đường cao phải xuất phát từ đỉnh tam giác còn trung trực chỉ dựa trên cạnh, không qua đỉnh.
Vì sao cần học kỹ về các đường đặc biệt này?
Nắm chắc cách phân biệt đường phân giác, đường trung tuyến, đường trung trực sẽ giúp bạn giải nhanh các bài toán hình học và ứng dụng trong các vấn đề thực tế như xác định vị trí cân bằng, tối ưu thiết kế kỹ thuật.
Hy vọng bài viết đã giúp bạn phân biệt đường phân giác, đường trung tuyến, đường trung trực một cách dễ hiểu và thực tế. Đừng quên chia sẻ, lưu lại bài viết hoặc truy cập blog Novateen để cập nhật thêm nhiều kiến thức bổ ích về học tập, tâm lý và phương pháp dạy con hiệu quả!